ในทางคณิตศาสตร์ "ฟังก์ชัน" บัญญัติขึ้นโดย ไลบ์นิซ ใน พ.ศ. 2237 เพื่ออธิบายปริมาณที่เกี่ยวข้องกับเส้นโค้ง เช่น ความชันของเส้นโค้ง หรือจุดบนเส้นโค้ง ฟังก์ชันที่ไลบ์นิซพิจารณานั้นในปัจจุบันเรียกว่า ฟังก์ชันที่หาอนุพันธ์ได้ และเป็นชนิดของฟังก์ชันที่มักจะแก้ด้วยผู้ที่ไม่ใช่นักคณิตศาสตร์ สำหรับฟังก์ชันชนิดนี้ เราสามารถพูดถึงลิมิตและอนุพันธ์ ซึ่งเป็นการทฤษฎีเซต พวกเขาได้พยายามนิยามวัตถุทางคณิตศาสตร์ทั้งหมดด้วย เซต ดีริคเลท และ โลบาเชฟสกี ได้ให้นิยามสมัยใหม่ของฟังก์ชันออกมาเกือบพร้อมๆกัน
ในคำนิยามนี้ ฟังก์ชันเป็นเพียงกรณีพิเศษของความสัมพันธ์ อย่างไรก็ตาม เป็นกรณีที่มีความน่าสนใจเป็นพิเศษ ความแตกต่างระหว่างคำนิยามสมัยใหม่กับคำนิยามของออยเลอร์นั้นเล็กน้อยมาก
แนวคิดของ ฟังก์ชัน ที่เป็นกฎในการคำนวณ แทนที่เป็นความสัมพันธ์ชนิดพิเศษนั้น อยู่ในคณิตตรรกศาสตร์ และวิทยาการคอมพิวเตอร์เชิงทฤษฎี ด้วยหลายระบบ รวมไปถึง แคลคูลัสแลมบ์ดา ทฤษฎีฟังก์ชันเวียนเกิด และเครื่องจักรทัวริง
ในคำนิยามนี้ ฟังก์ชันเป็นเพียงกรณีพิเศษของความสัมพันธ์ อย่างไรก็ตาม เป็นกรณีที่มีความน่าสนใจเป็นพิเศษ ความแตกต่างระหว่างคำนิยามสมัยใหม่กับคำนิยามของออยเลอร์นั้นเล็กน้อยมาก
แนวคิดของ ฟังก์ชัน ที่เป็นกฎในการคำนวณ แทนที่เป็นความสัมพันธ์ชนิดพิเศษนั้น อยู่ในคณิตตรรกศาสตร์ และวิทยาการคอมพิวเตอร์เชิงทฤษฎี ด้วยหลายระบบ รวมไปถึง แคลคูลัสแลมบ์ดา ทฤษฎีฟังก์ชันเวียนเกิด และเครื่องจักรทัวริง
นิยามอย่างเป็นรูปนัย
- สำหรับทุกค่า
 ใน
ใน  จะมี
จะมี  ใน
ใน  ซึ่ง
ซึ่ง 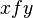 (
(  มีความสัมพันธ์
มีความสัมพันธ์  กับ
กับ  ) นั่นคือ สำหรับค่านำเข้าแต่ละค่า จะมีผลลัพธ์ใน
) นั่นคือ สำหรับค่านำเข้าแต่ละค่า จะมีผลลัพธ์ใน  อย่างน้อย
อย่างน้อย  ผลลัพธ์เสมอ
ผลลัพธ์เสมอ
- ถ้า
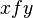 และ
และ 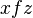 แล้ว
แล้ว 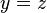 นั่นคือ ค่านำเข้าหลายค่าสามารถมีผลลัพธ์ได้ค่าเดียว แต่ค่านำเข้าค่าเดียวไม่ส อ่านเพิ่
นั่นคือ ค่านำเข้าหลายค่าสามารถมีผลลัพธ์ได้ค่าเดียว แต่ค่านำเข้าค่าเดียวไม่ส อ่านเพิ่




